Bellman-Ford's shortest paths Algorithm in C++

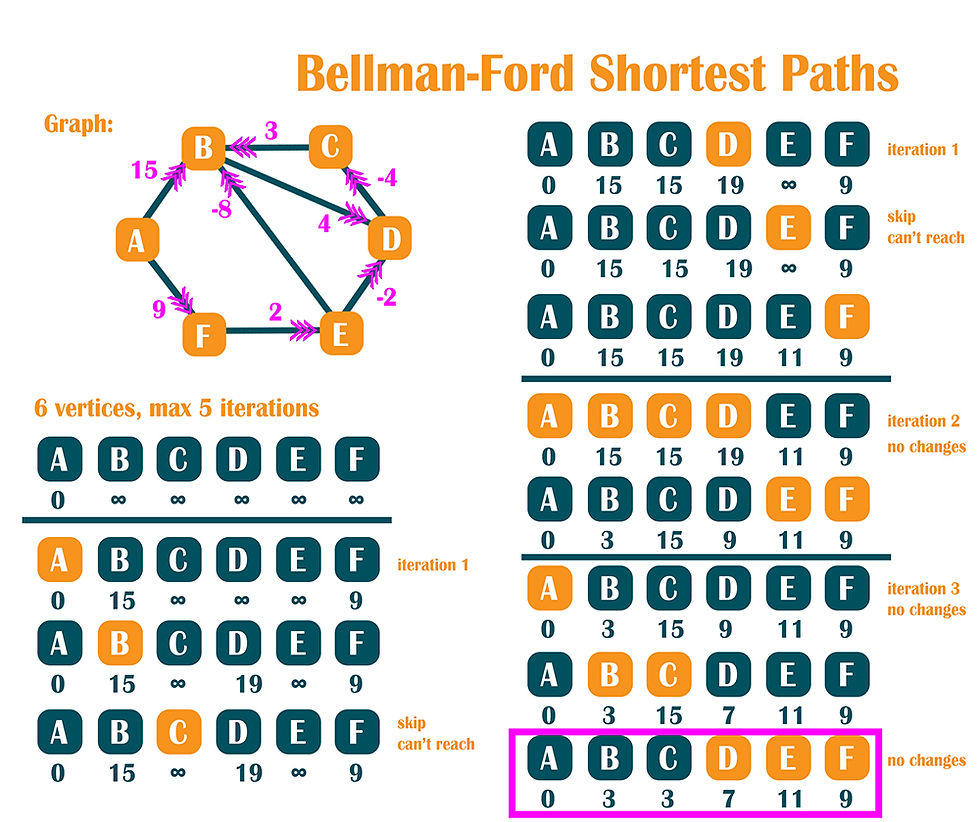
Using this algorithm, we find the shortest path from a node to all the other nodes in a weighted directed graph. It works with negative values of weights also as with positive values.

// Bellman-Ford's shortest paths algorithm.
#include <bits/stdc++.h>
using namespace std;

// define the global variables
#define Vertices 6
#define Edges 8
#define MAX 100000

int* BellmanFord(int graph[][3],int vertices, int edges, int startIndex)
{
    static int distances[Vertices];
    for (int i = 0; i < vertices; i++)
    {
        // initialize all distances to a large number, plus infinite
        distances[i] = MAX;
    }
    // The distance from start to start is 0
    distances[startIndex] = 0;

    // We need maximum of Vertex - 1 iterations
    for (int i = 0; i < vertices - 1; i++)
    {
        for (int j = 0; j < edges; j++)
        {
           if (distances[graph[j][0]] + graph[j][2] < distances[graph[j][1]])
           {
                distances[graph[j][1]] = distances[graph[j][0]] + graph[j][2];
            }
        }
    }

    // Check if there are cycles
    for (int i = 0; i < edges; i++)
    {
        int x = graph[i][0];
        int y = graph[i][1];
        int weight = graph[i][2];
        if (distances[x] != MAX && distances[x] + weight < distances[y])
        {
            cout << "This graph contains negative weight cycles"<< endl;
        }
    }
    return distances;
}

void printDistancesOfGrapf(int* arrayOfDistances, int vertices, int startIndex)
{
    cout << "Distance from vertex " << char(startIndex + 65) << endl;
    for (int i = 0; i < vertices; i++)
    {
         cout << char(i + 65) << ": " << arrayOfDistances[i] << endl;
    }
}

int main()
{
    int graph[][3] = { { 0, 1, 15 },
                       { 0, 5, 9 },
                       { 1, 3, 4 },
                       { 2, 1, 3 },
                       { 3, 2, -4 },
                       { 4, 1, -8 },
                       { 4, 3, -2 },
                       { 5, 4, 2 } };
    int startIndex = 0;

    int* newdistances;
    newdistances = BellmanFord(graph, Vertices, Edges, startIndex);
    printDistancesOfGrapf(newdistances, Vertices, startIndex);
    return 0;
}

Distance from vertex A A: 0 B: 3 C: 3 D: 7 E: 11 F: 9