Dijkstra’s Shortest Path Algorithm in C++

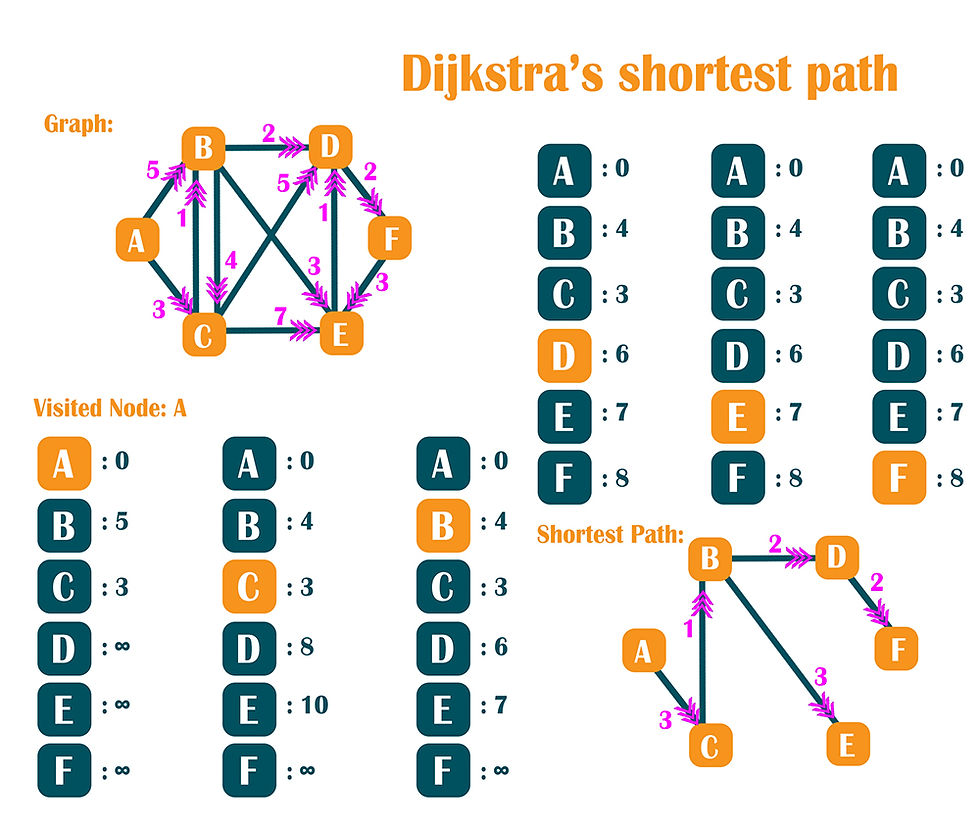
Dijkstra’s Shortest Path Algorithm is used to find the shortest path in a graph, from one node to every other node in a graph. Start with the first node, and find the next nodes that it can reach, note the distances. Pick the next node with a small value, and from this node calculate all the distances that this node can reach. Update the values if now they are smaller than the ones found in the previous search. Do this until you visit all the nodes and find all the smallest distances between the starting node and all the other ones.

// Dijkstra's shortest path

#include <iostream>
using namespace std;

// Number of nodes in the graph
#define Size 6

int minDistance(int distance[], bool shortestSet[])
{
    int minimum = INT_MAX;
    int minimum_index;

    for (int i = 0; i < Size; i++)
    {
         if (shortestSet[i] == false && distance[i] <= minimum)
         {
              minimum = distance[i];
              minimum_index = i;
         }
    }
    return minimum_index;
}

void printElementsOfGraph(int distance[])
{
    cout << "Node    Distance"<< endl;
    for (int i = 0; i < Size; i++)
    {
        // ASCII decimal: A = 65
        cout << char(i + 65);
        cout << "\t";
        cout << distance[i] << endl;
    }
}

void dijkstraShortestPath(int graph[Size][Size], int sourceNode)
{
    // The output array with the shortest paths
    int distance[Size];
    bool shortestSet[Size];

    // Initialize all distances as INFINITE and shortestSet[] as false
    for (int i = 0; i < Size; i++)
    {
        distance[i] = INT_MAX;
        shortestSet[i] = false;
    }
    // Distance from source node to itself is always 0
    distance[sourceNode] = 0;

    // Find shortest path for all nodes
    for (int i = 0; i < Size - 1; i++)
    {
        int node = minDistance(distance, shortestSet);
        // Mark the picked node as processed
        shortestSet[node] = true;

        // Update the distances of path
        for (int j = 0; j < Size; j++)
        {
            if (!shortestSet[j] && graph[node][j] && distance[node] != INT_MAX
                && distance[node] + graph[node][j] < distance[j])
                {
                   distance[j] = distance[node] + graph[node][j];
                }
        }
    }
    printElementsOfGraph(distance);
}

int main()
{
    int graph[Size][Size] = { { 0, 5, 3, 0, 0, 0 },
                            { 0, 0, 4, 2, 3, 0 },
                            { 0, 1, 5, 0, 7, 0 },
                            { 0, 0, 0, 0, 0, 2 },
                            { 0, 0, 0, 1, 0, 0 },
                            { 0, 0, 0, 0, 3, 0 } };
    int sourceNode = 0;
    dijkstraShortestPath(graph, sourceNode);
    return 0;
}

Node Distance A 0 B 4 C 3 D 6 E 7 F 8