Floyd Warshall Algorithm in C++

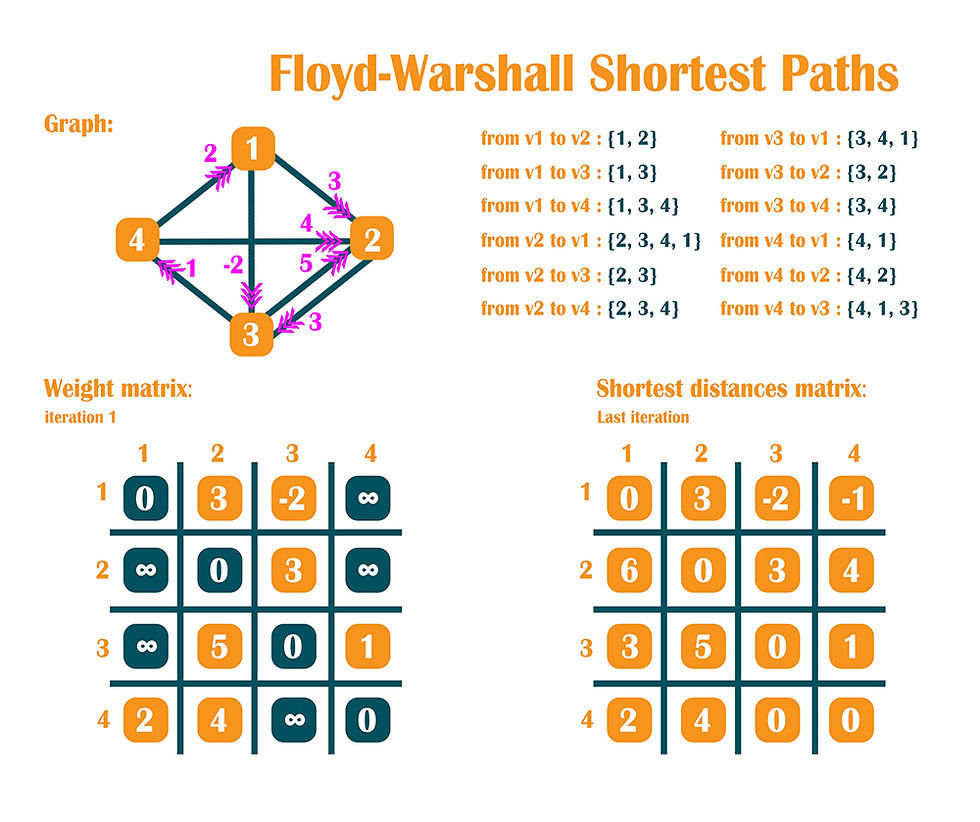
This algorithm is used to find the shortest path between all pairs of vertices, including negative edges.

// Floyd-Warshall Shortest Paths Algorithm

#include <iostream>
#include <climits>
#include <iomanip>
using namespace std;

#define Vertices 4

// Print path from vertex
void printPath(int pathMatrix[][Vertices], int i, int j)
{
	if (pathMatrix[i][j] == i)
    {
        return;
    }

	printPath(pathMatrix, i, pathMatrix[i][j]);
	cout << pathMatrix[i][j] + 1 << " ";
}

void printSolution(int costMatrix[Vertices][Vertices], int pathMatrix[Vertices][Vertices])
{
    // print matrix of shortest paths
    cout << "Shortest Paths Values Matrix: " << endl;
	for (int i = 0; i < Vertices; i++)
	{
		for (int j = 0; j < Vertices; j++)
		{
			if (costMatrix[i][j] == INT_MAX)
            {
                cout << setw(4) << "inf";
            }
			else
            {
                cout << setw(4) << costMatrix[i][j];
            }
		}
		cout << endl;
	}

	// print info for each vertex
	cout << endl;
	cout << "Shortest Paths: " << endl;
	for (int i = 0; i < Vertices; i++)
	{
		for (int j = 0; j < Vertices; j++)
		{
			if (j != i && pathMatrix[i][j] != -1)
			{
				cout << "From vertex " << i + 1 << " to vertex " << j + 1 << ": " << i + 1 << " ";
				printPath(pathMatrix, i, j);
				cout << j + 1 << endl;
			}
		}
	}
}

void FloydWarshall(int matrix[][Vertices])
{

	int costMatrix[Vertices][Vertices];
	int pathMatrix[Vertices][Vertices];

	// initialize the 2 matrices
	for (int i = 0; i < Vertices; i++)
	{
		for (int j = 0; j < Vertices; j++)
		{
			// the initial cost is the original weight of the matrix
			costMatrix[i][j] = matrix[i][j];

			if (i == j)
            {
                pathMatrix[i][j] = 0;
            }
			else if (costMatrix[i][j] != INT_MAX)
            {
                pathMatrix[i][j] = i;
            }
			else
            {
				pathMatrix[i][j] = -1;
            }
		}
	}

	// Floyd-Warshall
	for (int i = 0; i < Vertices; i++)
	{
		for (int j = 0; j < Vertices; j++)
		{
			for (int k = 0; k < Vertices; k++)
			{
				if (costMatrix[j][i] != INT_MAX && costMatrix[i][k] != INT_MAX && costMatrix[j][i] + costMatrix[i][k] < costMatrix[j][k])
				{
					costMatrix[j][k] = costMatrix[j][i] + costMatrix[i][k];
					pathMatrix[j][k] = pathMatrix[i][k];
				}
			}
			if (costMatrix[j][j] < 0)
			{
				cout << "Negative Weight Cycle Found!";
				return;
			}
		}
	}
	printSolution(costMatrix, pathMatrix);
}

int main()
{
	int matrix[Vertices][Vertices] =
	{
		{ 0,       3,   -2,     INT_MAX },
		{ INT_MAX, 0,    3,     INT_MAX },
		{ INT_MAX, 5,    0,     1 },
		{ 2,       4, INT_MAX,  0 }
	};
	FloydWarshall(matrix);
}

Shortest Paths Values Matrix:

   0   3  -2  -1

   6   0   3   4

   3   5   0   1

   2   4   0   0

Shortest Paths:

From vertex 1 to vertex 2: 1 2

From vertex 1 to vertex 3: 1 3

From vertex 1 to vertex 4: 1 3 4

From vertex 2 to vertex 1: 2 3 4 1

From vertex 2 to vertex 3: 2 3

From vertex 2 to vertex 4: 2 3 4

From vertex 3 to vertex 1: 3 4 1

From vertex 3 to vertex 2: 3 2

From vertex 3 to vertex 4: 3 4

From vertex 4 to vertex 1: 4 1

From vertex 4 to vertex 2: 4 2

From vertex 4 to vertex 3: 4 1 3