Longest Increasing Sub-sequence in C++

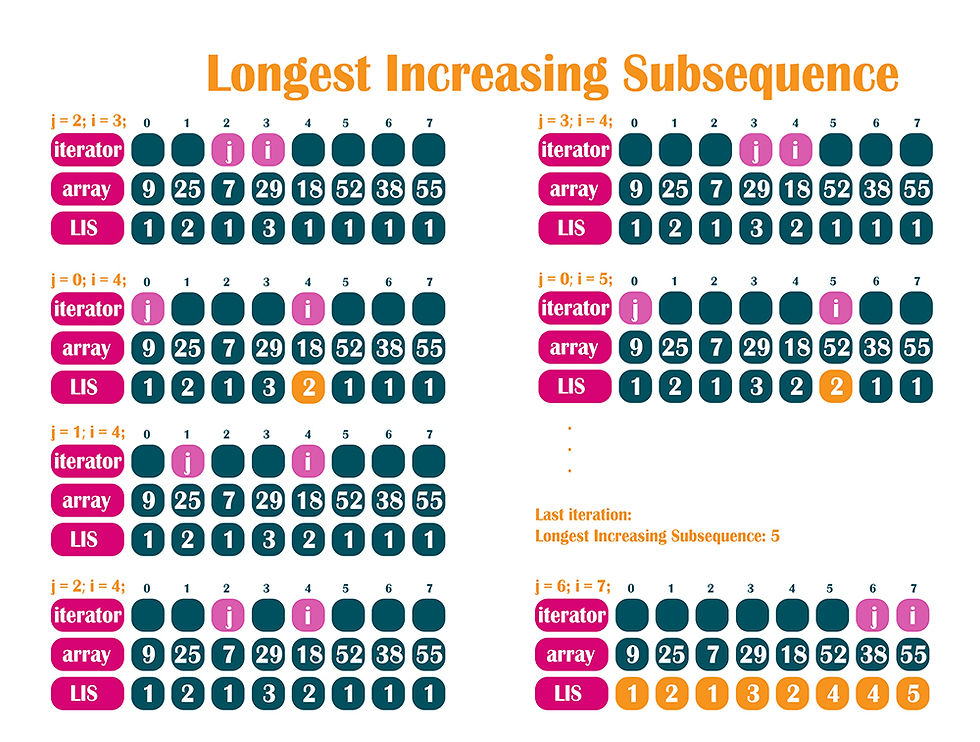
Using this algorithm we can find the longest increasing subsequence from a given array. This means that we will find the numbers that are found in a sorted way, from smallest to largest, that are not necessarily adjacent. For example, from 6, 5, 9, the longest increasing subsequence is of value 2, being created by 6 and 9, or by 5 and 9.

// Longest Increasing Subsequence
#include <stdio.h>
#include <stdlib.h>

int longestIncreasingSubsequence(int arrayOfNumbers[], int numberOfElements)
{
    int *lis;
    int maxLength = 0;
    lis = (int*)malloc(sizeof(int) * numberOfElements);

    for (int i = 0; i < numberOfElements; i++)
    {
        lis[i] = 1;
    }

    for (int i = 1; i < numberOfElements; i++)
    {
         for (int j = 0; j < i; j++)
         {
             if (arrayOfNumbers[i] > arrayOfNumbers[j] && lis[i] < lis[j] + 1)
             {
                 lis[i] = lis[j] + 1;
             }
         }
    }

    for (int i = 0; i < numberOfElements; i++)
    {
        if (maxLength < lis[i])
        {
            maxLength = lis[i];
        }
    }
    free(lis);

    return maxLength;
}

int main()
{
    int arrayOfNumbers[] = { 9, 25, 7, 29, 18, 52, 38, 55 };
    int numberOfElements = sizeof(arrayOfNumbers) / sizeof(arrayOfNumbers[0]);
    int laxLength = longestIncreasingSubsequence(arrayOfNumbers, numberOfElements);
    printf("The length of the longest increasing subsequence is %d.", laxLength);
    return 0;
}

The   length of the longest increasing subsequence is 5.