Minimum Cost Polygon Triangulation in C++

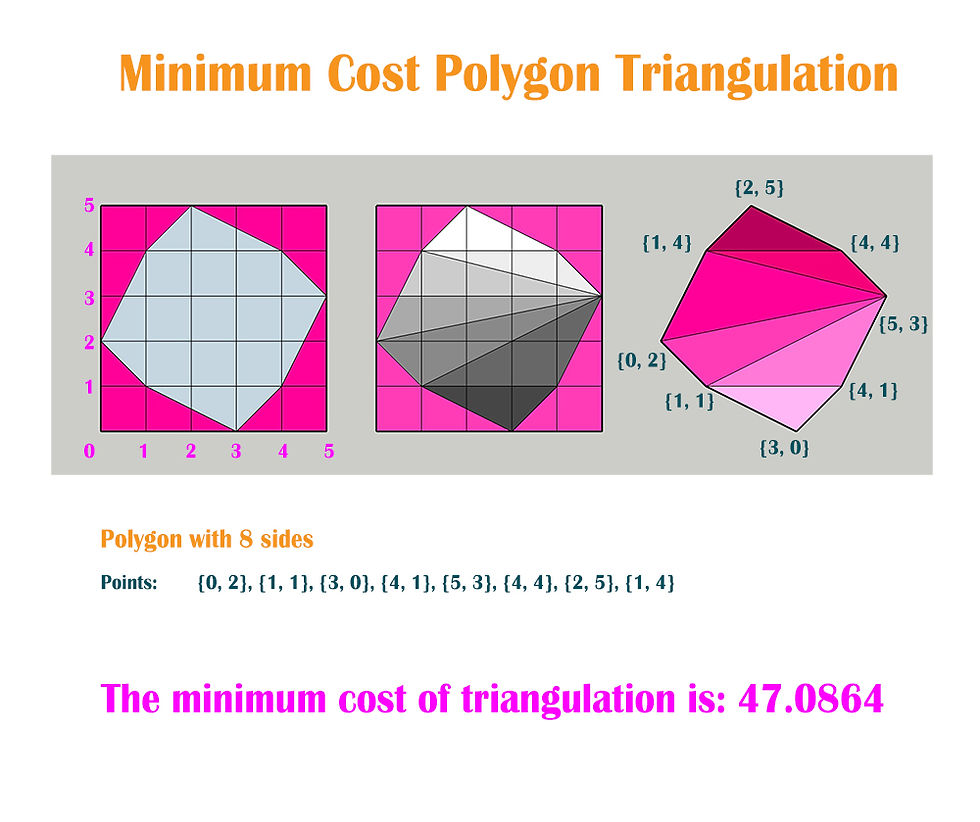
Having a given polygon, divide it using triangulation between all points, having the minimum cost. This means that we have to divide the polygon into triangles, that have no overlapping sides. We are reducing the complex shape into more simpler shapes.

Every triangulation of an n-gon has exactly n − 2 triangles. This means that a polygon has 13 edges, then it will have 11 triangles.

First divide the polygon using a triangle and create two separate polygons. Then divide each new polygon.

// Minimum Cost Polygon Triangulation
#include <iostream>
#include <cmath>
#define MAX 100000000.0
using namespace std;

struct Point {
   int x, y;
};

double distanceBetweenPoints(Point p1, Point p2)
{
   return sqrt(pow((p1.x - p2.x), 2) + pow((p1.y - p2.y), 2));
}

double perimeterOfTriangle(Point triangle[], int i, int j, int k)
{
   Point p1 = triangle[i];
   Point p2 = triangle[j];
   Point p3 = triangle[k];
   return distanceBetweenPoints(p1, p2) + distanceBetweenPoints(p2, p3) + distanceBetweenPoints(p3, p1);
}

double minimumCostPolygonTriangulation(Point polygon[], int numberOfPoints)
{
    if (numberOfPoints < 3)
    {
        return 0;
    }

   double table[numberOfPoints][numberOfPoints];

   for (int gap = 0; gap < numberOfPoints; gap++)
    {
      for (int i = 0, j = gap; j < numberOfPoints; i++, j++)
      {
         if (j < i + 2)
         {
              table[i][j] = 0.0;
         }
         else
        {
            table[i][j] = MAX;

            for (int k = i + 1; k < j; k++)
            {
               double minValue = table[i][k] + table[k][j] + perimeterOfTriangle(polygon, i, j, k);
               if (table[i][j] > minValue)
               {
                    table[i][j] = minValue;
               }
            }
         }
      }
   }
   return  table[0][numberOfPoints - 1];
}

int main() {
   Point points[] = {{0, 2}, {1, 1}, {3, 0}, {4, 1}, {5, 3}, {4, 4}, {2, 5}, {1, 4}};
   int numberOfPoints = 8;
   cout <<"The minimum cost of triangulation is: " <<minimumCostPolygonTriangulation(points, numberOfPoints);
}

The minimum cost of triangulation is: 47.0864