Prim’s Minimum Spanning Tree Algorithm in C++

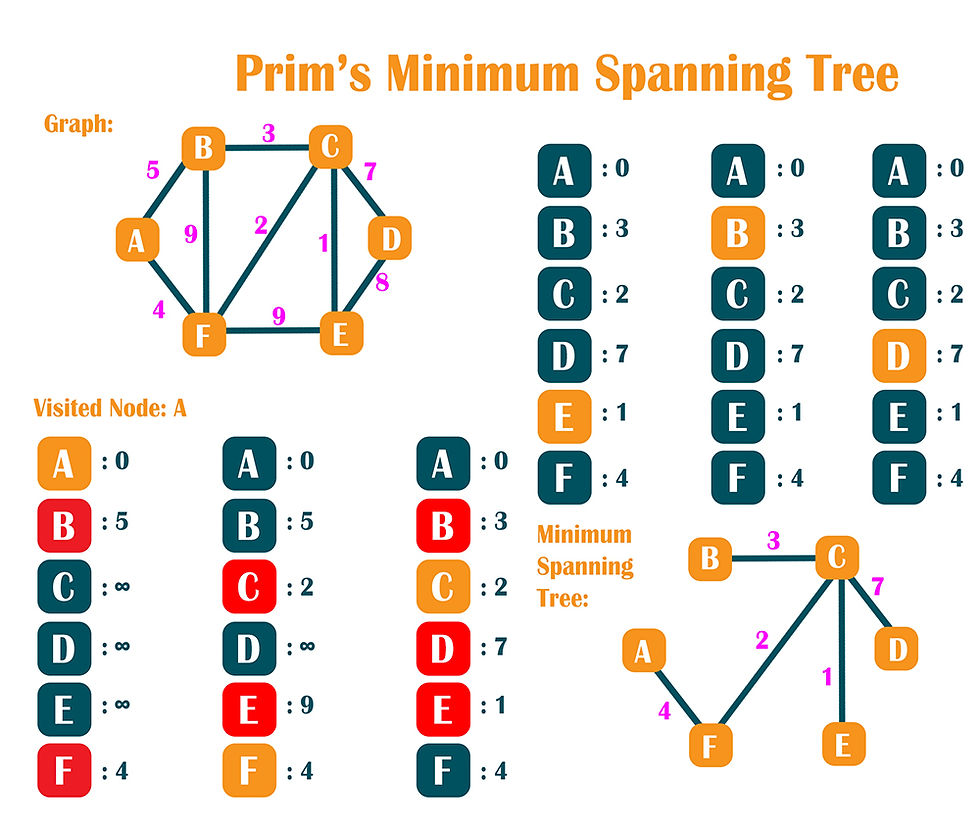
A spanning tree is a subgraph of an existing graph that is a tree and connects all the nodes. There can be many spanning trees in a graph. Prim’s algorithm finds the minimum spanning tree, whose sum of weights of edges is minimum.

// Prim’s Minimum Spanning Tree Algorithm

#include <bits/stdc++.h>
using namespace std;

// Number of nodes in the graph
#define Nodes 6

// Find the minimum value node
int mininumKey(int keys[], bool minimumSpanningTreeSet[])
{
    int mininumValue = INT_MAX;
    int minimumIndex;

    for (int i = 0; i < Nodes; i++)
    {
        if (minimumSpanningTreeSet[i] == false && keys[i] < mininumValue)
        {
            mininumValue = keys[i];
            minimumIndex = i;
        }
    }
    return minimumIndex;
}

// Print the solution
void printEdgeWidth(int parent[], int graph[Nodes][Nodes])
{
    cout<<"Edge \tWeight\n";
    for (int i = 1; i < Nodes; i++)
    {
        char firstNode = parent[i] + 65;
        char secondNode = i + 65;
        cout<<firstNode<<" - "<<secondNode<<" \t"<<graph[i][parent[i]]<<" \n";
    }
}

void primMinimumSpanningTree(int graph[Nodes][Nodes])
{
    int parentGraph[Nodes];
    int keys[Nodes];
    bool minimumSpanningTreeSet[Nodes];

    // Initialize all values as +infinite
    for (int i = 0; i < Nodes; i++)
    {
        keys[i] = INT_MAX;
        minimumSpanningTreeSet[i] = false;
    }

    keys[0] = 0;
    parentGraph[0] = -1;

    for (int i = 0; i < Nodes - 1; i++)
    {
        int minKey = mininumKey(keys, minimumSpanningTreeSet);
        minimumSpanningTreeSet[minKey] = true;

        // Update the key value and parent index of the adjacent nodes of the picked node.
        for (int i = 0; i < Nodes; i++)
        {
            if (graph[minKey][i] && minimumSpanningTreeSet[i] == false && graph[minKey][i] < keys[i])
            {
                parentGraph[i] = minKey;
                keys[i] = graph[minKey][i];
            }
        }
    }

    // print the constructed MST
    printEdgeWidth(parentGraph, graph);
}

int main()
{
    int graph[Nodes][Nodes] = { { 0, 5, 0, 0, 0, 4 },
                                { 5, 0, 3, 0, 0, 9 },
                                { 0, 3, 0, 7, 1, 2 },
                                { 0, 0, 7, 8, 0, 0 },
                                { 0, 0, 1, 0, 8, 9 },
                                { 4, 9, 2, 0, 9, 0 } };

    primMinimumSpanningTree(graph);
    return 0;
}

Edge    Weight
C - B   3
F - C   2
C - D   7
C - E   1
A - F   4